Linking soft computing to art: introduction of efficient k-continuous line drawing
Yanjie Zhou, Gyu M. Lee
Applied Soft Computing


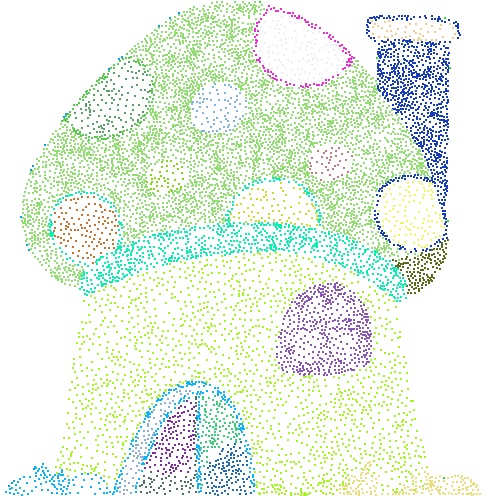

Input image, segmentation result, stippling result, k-CLD result.
Abstract
Continuous line drawing (CLD) is a technique used in the field of art, in which the pen does not leave the paper until the sketch is completed. In this study, a novel technique, k-continuous line drawing (k-CLD), is proposed; this technique enables a visual image to comprise k closed non-intersecting lines. k-CLD involves the following challenges: 1) partitioning the target image into k regions, 2) stippling each region without distorting the target image, and 3) connecting the stippled dots in each region using a single closed, non-intersecting line. This study identifies and implements efficient algorithms to produce high-quality k- CLDs. Further, an improvement to the graph-based image segmentation algorithm has been proposed using the Minkowski distance to evaluate dissimilarity difference and demonstrated its effectiveness to partition the target image into k regions. Next, well-spaced stippled dots were generated in each region using a weighted Voronoi diagram. Finally, the stippled dots were connected by a single non-intersecting line, obtained by solving a traveling salesman problem (TSP) in each region. The metaheuristic to solve the TSP was an ant colony system algorithm. The proposed methodologies were tested on a wide variety of images to demonstrate their effectiveness and efficiency.
Research Highlights
References
-
Linking soft computing to art: introduction of efficient k-continuous line drawing, Yanjie Zhou, Gyu M. Lee. Applied Soft Computing, 68, 932–943.

- Linking the optimization to the art; an efficient k-continuous line drawing using image segmentation, stippling, and the traveling salesman problem. Yanjie Zhou, Gyu M. Lee. The 2016 International Symposium on Semiconductor Manufacturing Intelligence (ISMI2016)